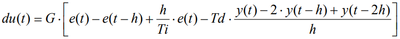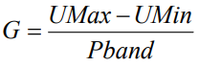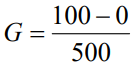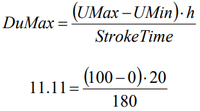Issue
Supplemental Documentation on the Menta/Function Block PID simple blocks
Product Line
TAC Vista, EcoStruxure Building Operation
Environment
Menta/Function Block editor
Cause
The document below is intended to clarify some of the more subtle aspects of the Menta/Function Block PID blocks and when/how to use them.
Resolution
A Brief Overview of PID Control
Proportional-integral-derivative (PID) control is a generic feedback control loop algorithm. A PID controller calculates the error from the desired setpoint of a measured variable. It then adjusts the control output accordingly to try and minimize this error. Parameters used in the calculation must be tuned according to the system they are employed to control.
The three prominent parameters are the proportional, integral, and derivative values. The proportional value affects the change in the output signal based upon the current error from setpoint. The integral value works based on the sum of the most recent errors. The derivative value reacts based on the rate at which the error has been changing. The weighted sum of these three actions is used to adjust the control output.
The most typical application used in HVAC controls is actually a proportional-integral control with no derivative influence (PI). Derivative action is very sensitive to measurement noise, and generally considered too complex for the relatively limited benefit to slower, more easily controlled loops.
Three Types of PID Blocks in Menta
Menta has three different simple blocks for PID control. They are: PIDI, PIDP, and PIDA (links to Web Help).
PIDI
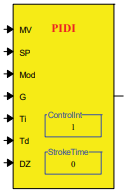
Input parameters to the PIDI will influence the operation of the controlled output in the same way as the analog PID blocks. The output, however, will not show a percentage. The end user will only be able to force an “open” or “close” command to the actuator – not set it to a desired percentage. Examples of how to use PIDI are explored later in the document.
PIDP
PIDP differs from PIDA in 4 distinct ways:
- PIDP will remain in saturation for a longer time than PIDA. The integral portion of the calculation keeps a running sum of previous error adjustments. Because of this, it can “wind up” a stored integral response. There is an anti-wind up mechanism to combat the effect, but PIDA has no wind up at all.
- In PIDP, a change in the setpoint value will not cause a step change when using PI or PID control. The measured error is not from the setpoint input, but rather from the last sampled measured value. The PID block samples a measured variable any time it is inside the deadzone. The allows for the calculation’s setpoint to equal the edge of the deadzone and have a less dramatic response to exiting the deadzone. The other time it will sample a new measured variable is any time a control coefficient is changed. This is an important distinction to be aware of during tuning operations. It may be useful to force the measured variable equal to setpoint after altering tuning parameters.
- The tracking of the tracking signal is not instantaneous in PIDP, as opposed to PIDA. Looping back the output to the TSg tracking signal feedback input will not cause the PID to stay synched with an overridden output. Additional logic is needed to switch the Mode to 0 for one program cycle in order to lock in the feedback signal any time it does not equal the output signal.
- The D-part is not as sensitive to measurement noise in PIDP as in PIDA.
PIDA
where e is the control error, y is the measured value (MV), G is the controller Gain, Ti is the integral time, Td is the derivative time and h is the Control Interval (ControlInt), i.e. the time between two successive updates of the controller output signal.
While analyzing and understanding this formula is beneficial to fully understanding the PID simple block, do not get too mired in the details. This document will help to demystify input parameters to make the PID work in a number of situations.
For the purpose of this document, a PIDA will be assumed for all applications.
Inputs to the PIDA Block
MV
Measured value is the process variable for the PID controller. It is an input value of type Real. Examples of this would be a room temperature, a return air CO2 level, or a hot water differential pressure.
SP
Setpoint is the desired value of the measured value. It is an input value of type Real. It could be a static value (Operator “Real const”), adjustable from the front end (Simple Block “PVR”), a stepping value, or a modulating value. If the setpoint is likely to change often, it is recommended to use the PIDA block as opposed to PIDP.
Mod
The mode input to the PID block will control its action and enable or disable the control output. It is an input value of type Integer. There are four possible modes:
- Mode = 0
- Web Help lists this mode as, “Off, controller stopped.” A more accurate description would be, “The value present at the TSg input will pass through to the output.” If the looped back output value is not changing, then the PID output will freeze.
- Mode = 1
- Normal control. A new output value will be calculated on every Control Interval.
- Mode = 2
- Controller output forced to UMax. This could be used on a hot water valve when freeze protection is enabled.
- Mode = 3
- Controller output forced to UMin. This typically represents the “off” position of a PID.
G
Gain is the proportional parameter of the PID control. It is an input value of type Real. It is represented by the following equation:
To arrive at an appropriate default value for Gain, three parameters must be considered: UMax, UMin, and proportional band. In typical applications, UMin and UMax will be 0% and 100%, respectively. This is because most valve or damper actuators are going to control between 0-100%. For the following examples, this will be assumed, but do not discount the effect it will have on default Gain parameters if these values change (such as in a cascade control application).
Appropriate default parameters are merely in the same mathematical order of magnitude as the final tuned value. Rarely will the default parameter result in perfect operation of the control loop. It is only intended to get close enough to provide decently steady control until proper tuning can take place.
It is usually easier to think in terms of proportional band than proportional Gain. Consider a room temperature. What would be an appropriate band around the setpoint to maintain? Perhaps ±5°F. If ±5°F is selected, that would result in a 10°F proportional band. Plug that into the equation along with the assumed UMin and UMax values:
This would result in a default Gain of 10.
It is important to remember that Gain is a unit-less value. A Gain of 10 is neither large nor small – merely relative to the process variable and anticipated error from setpoint. Consider a PID controlling an outside air damper to maintain an outside air flow of 1000cfm. Would a proportional band of 10cfm make sense in this situation? Probably not. A more appropriate value might be a band of 500cfm. Plug this into the same equation as before:
In the case of air flow control, because the process variable and anticipated error from setpoint are so much larger than in temperature control, a more appropriate default Gain would be 0.2.
In a third situation, consider a PID controlling static air pressure in a supply duct by modulating a variable speed fan. A proportional band of 500”wc would not make sense. A band of 0.8”wc might be more appropriate.
In the instance of static air pressure, a default Gain of 125 would be suitable. Comparing these three situations with Gains of 0.2, 10, and 125, they will all have relatively similar speeds in the control loop. Just by glancing at these values alone, it cannot be said that any of them are “bigger” or “faster” than the others without a more in depth mathematical analysis.
In addition to the value of the Gain, the sign is also important. Positive values represent reverse acting PIDs like a hot water valve where the signal to the valve will decrease as the room temperature increases. Negative values represent direct acting PIDs like a chilled water valve where the signal to the valve will increase as the room temperature increases.
To avoid confusion at the front end, and reduce the possibility that end users will accidentally reverse the action of a PID, it is best practice to always use a positive value PVR to represent the value of the Gain. Then use an Expression absolute value operator “ABS()” to remove any sign and apply a negative value when necessary. Using this method, the Gain from the front end will always appear as a positive value and no consideration for the proper action of the PID will need to be taken after the programming phase is complete.
Ti
Ti is the integral time, or the integral portion of the PID control. It is an input value of type Real. Adding integral control to a straight proportional algorithm helps to avoid “controlling to an offset.” It is theoretically possible that a chilled water valve at 40% is exactly the amount of chilled water required to maintain a supply air temperature of 58°F, even if the setpoint is 55°F. If the error in the signal never changes, then the proportional algorithm will not change the output signal. And an offset has been achieved and will now be maintained indefinitely.
Integral time will eliminate this possibility. Every Control Interval that the temperature remains above the setpoint, integral control will add a little more to the control output. This will cause the measured variable to always approach the setpoint. Because this value does have units (seconds) it is possible to compare one integral time value to the next.
Ti is inversely proportional to the integral effect in the formulation of the next control output. In general, the smaller the Ti value, the more integral control will affect the control output. A value of 50 seconds would have a very large impact on the output. A value of 2500 seconds would hardly affect the control output at all. The exception to this rule is that a value of 0 seconds will disable integral control. Typical default values fall anywhere between 250-1000 seconds.
Some PID solutions may be susceptible to “integral wind up” where the internal calculation desires and integral response beyond the output limits. When the control signal reverses, the integral wind up must be reversed before the output sees the change. In the PIDA algorithm, integral wind up is not a concern.
Td
Derivative time is also measured in seconds and represents the D portion of the PID. It is an input value of type Real. Derivative control is generally considered too complex and sensitive to measurement noise to be of sufficient benefit to HVAC control. A Simple Block “PVR” set to a value of 0 seconds will disable derivative control, but allow the tuner to add derivative control if desired.
DZ
Dead zone refers to the amount above and below the desired setpoint that will result in no change to the control output. It is an input value of type Real. This differs from the concept of a proportional band in that it is not centered around the value. While a proportional band of 10°F represents ±5°F around setpoint, a dead zone of 10°F would represent ±10°F around setpoint.
A dead zone is helpful to reduce “hunting” of the control output where it repeatedly rises and falls when a steady output would cause the control variable to steady out. Typical values depend on the process variable. For a supply air temperature, anywhere from 0.25°F to 0.5°F would suffice. For outside air flow, anywhere from 50cfm to 100cfm might be appropriate. In a supply air static pressure control loop, limiting the dead zone to 0.1”wc would suffice.
TSg
TSg is short for tracking signal. It is an input value of type Real. The internal equation uses this as the value of the previous control signal. It should be looped back to the PID from the output signal. This might be directly from the output of the PID, or it may be after some external logic.
The TSg input can be used in another way as well. When the PID is in Mode 0, the TSg value passes directly through to the output signal. By setting the PID to Mode 0 for the first second of a control period, initial positions other than UMin or UMax can be achieved. It can also be used to keep a PID in synch with an output that has been overridden by the front end.
If the PID is controlling a physical output AO, then the output of the AO should be looped back to the PID.
Configuration Parameters of the PIDA Block
ControlInt
The Control Interval represents the number of seconds in between each successive calculation of outputs. If this value is set to 0 seconds, then the Control Interval will match the cycle time of the application.
The Control Interval should be thought of in terms of how long a change in the control output will take before the impact is realized on the measured variable. Consider three scenarios:
- Scenario 1: A variable speed drive modulates a pump speed to maintain chilled water differential pressure. Because water is incompressible, a change in the pump speed results in an almost immediate change in the pressure. A Control Interval of 1 second is appropriate in this scenario.
- Scenario 2: A chilled water valve modulates to maintain a supply air temperature setpoint. The supply air temperature sensor is a few feet down the duct from the chilled water coil. A PID controller moves the chilled water valve from 0% to 10%. How long will it take before the supply air temperature starts to fall? Granted, there are several X factors in this equation, but a good guess might be around 20 seconds. A Control Interval of 20 seconds is appropriate in this scenario.
- Scenario 3: A supply air temperature setpoint modulates to maintain a large auditorium's temperature setpoint in a classic cascade control configuration. A chilled water valve then modulates to maintain the supply air temperature setpoint. Room temperature dictates that the supply air temperature setpoint should drop from 60°F to 55°F. How long will it take before this change in setpoint causes the room temperature to fall? It may take a full minute, perhaps even several minutes before that change has an affect at the room temperature sensor. A Control Interval of 80 seconds, while seeming very slow, is perfectly appropriate here.
Correctly configured Control Intervals will allow one change in position to have an effect on the measured variable before a second (or third, or fourth...) change is made. A proper Control Interval will stop the valve from overshooting unnecessarily.
UMin
UMin is the minimum possible output of a PID controller. In most applications (valve and damper actuators) this will be set to 0%. In the case of a cascade control supply air setpoint PID, it might be set to 50°F.
If the hardware output has a minimum position (say on an outside air damper), it is best to accomplish this with secondary logic as opposed to using the PID UMin. Otherwise if the PID is made public to the front end, the user will never see this value drop to 0, even if the control output is at 0.
UMax
UMax is the maximum possible output of a PID controller. In most applications (valve and damper actuators) this will be set to 100%. In the case of a cascade control supply air setpoint PID, it might be set to 90°F.
StrokeTime
The name Stroke Time refers to the manufacturer specified stroke time of a physical actuator. By setting the PID to the same stroke time as the valve it is controlling, it is guaranteed not to “wind up” faster than it is possible for the valve to react. Whenever possible, set the stroke time to match the physical stroke time of the actuator it is controlling.
However, stroke time can be thought of in another way. It is used to calculate DuMax, the maximum rate of change of the controller output during one Control Interval. In the case of a chilled water valve that modulates between 0% and 100% with a Control Interval of 20 seconds, see how a stroke time of 180 seconds affects the DuMax:
A stroke time of 0 seconds will not limit the rate of change at all in the controller. Based on the error and the Gain, it could potentially jump the full 100% stroke at once. By setting the stroke time to 180 seconds, the amount that the control signal can move every 20 seconds is now limited to 11.11%.
It is not proper practice to employ stroke time as a tuning mechanism of a PID. It should be set prior to and independent from the tuning process.
Output of a PIDA Block
The output of a PIDA block will usually control a hardware output from a Xenta controller. Because of this, it is typically connected to a Menta Simple Block “AO.” In Function Block it may be output to an analog value or hardware output.
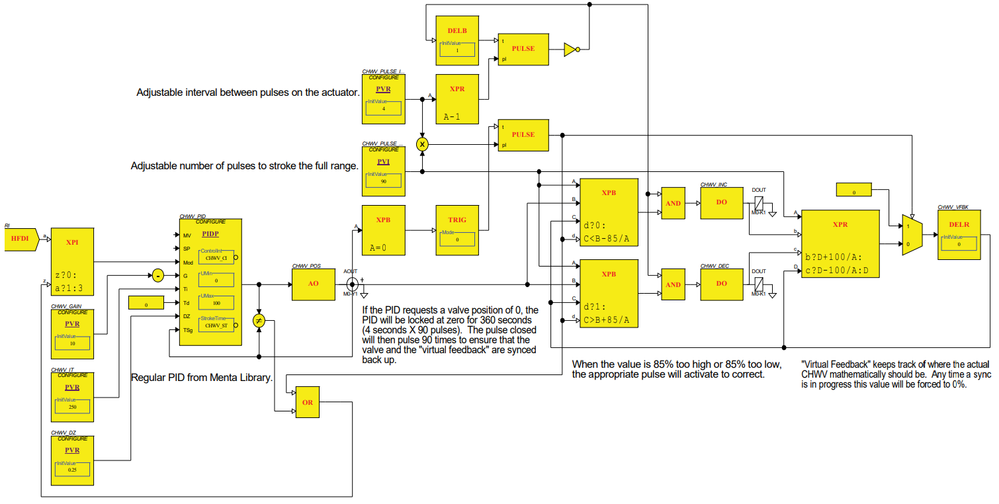
Output of a PIDI Block
A PIDI controls a floating actuator using two Simple Block “DOPU” digital pulse outputs. The PIDI will output a value between -1 and 1, which the DOPU block converts into the appropriate pulse lengths. Inverting the decrease signal will pulse the actuator closed when the output of the PIDI is negative.
The downside to PIDI control is that there is no percentage value to report to the front end about the position of the actuator. This is why use of the PIDI is somewhat rare. The same control can be accomplished using a PIDA with some external logic to pulse the floating actuator open and closed. Using a “virtual feedback” signal to mathematically monitor the assumed position of the floating actuator allows the end-user to view a percentage open signal for the actuator. It also allows them to override the Not-Connected AO to a certain position and have the floating actuator travel to that position just as an analog output would. The following example converts a Not-Connected AO from a PIDA into pulse output DOs from the controller.
Public Signals and Public Constants
All of the parameters that go into the operation of a PID need to be considered when tuning its operation. Eventually, one will come to the question of what parameters need to be made available from the front end. While some thoughts might end up on the well-meaning, under-trained end-user who could potentially wreak havoc by adjusting values, it is more important to consider the startup technician.
If a value is not public from the front end, then a download must be performed to make any changes to any values. By making every parameters public by default (and only selectively removing certain parameters during exceptions) less time will be spent in the field during start up. After the PIDs have been tuned, it is always possible to remove certain values from being public.
The exceptions are UMin and UMax, which when controlling a valve or a damper are almost always 0% and 100%. If desired, these can usually be hard-coded into the PID with little consideration. However, they can also be made available from the front end with little or no ill effects.
Floating, PID, or Cascade Control
There are three main control loop algorithms to consider when programming. Which one best suits the application is really a factor of the control loop speed. Consider the three options:
Floating
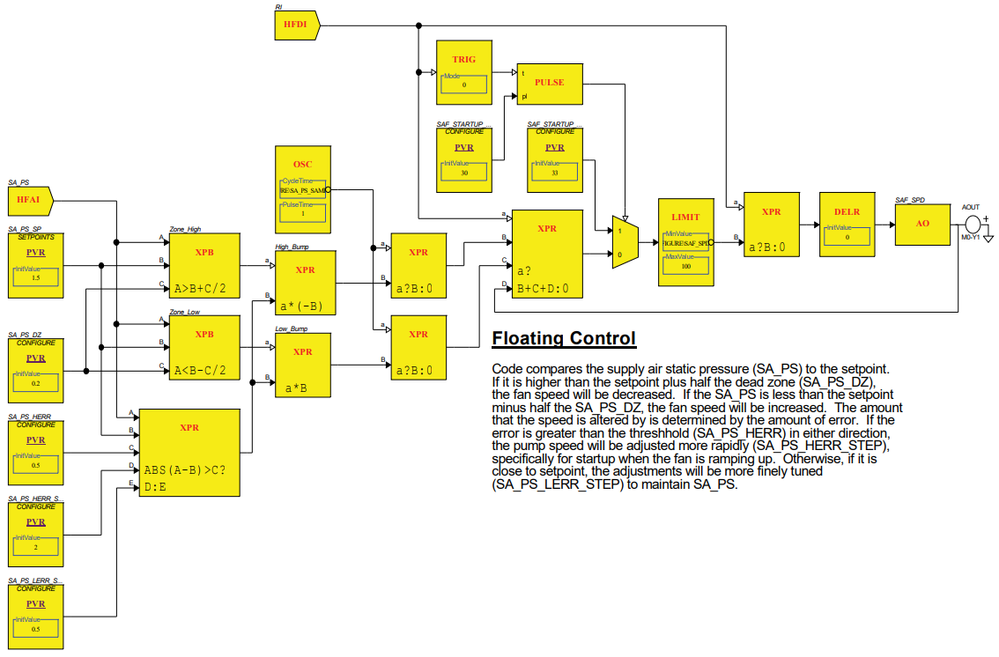
Floating control (also called bump control) involves making small, measured adjustments to the control signal on specified intervals. This is usually the best option any time a variable speed drive is involved. This is because these drives typically control supply fan static pressure or hot/cold water pump differential pressure.
Both of these are very fast control loops. A slight change in the speed of the drive results in an almost instantaneous change in the measured variable. Floating control reacts more gradually to these quick changes. It compares the measured variable to the setpoint, and if it is too high, it bumps the control signal down a little bit. If the measured variable is too low, it bumps the control signal up a little bit.
PIDs can (and often have been) used successfully to control very fast control loops. However, they are typically tuned to closely resemble floating control – low Control Interval, very little proportional control, very high integral control. In the end, it may be easier for a technician to understand and adjust “1% every 5 seconds” than “a Gain of 125 and an integral time of 175 seconds.”
The other advantage to floating control is its adaptability. When tuning a PID, it is tuned to one exact set of circumstances – a certain load on the building, a certain volume of piping, etc. If enough of those conditions change by enough, the PID can be sent into oscillations. Floating control will not be affected by these changes. Consider a PID tuned to control a chilled water pump, which maintains differential pressure during the winter when loads are low. During the summer, a manual valve is opened to provide cooling to the athletics storage shed that was unoccupied all winter. This will increase both the demand for cooling and the volume of the pipe. This could potentially render the PID useless. However, a floating control will not react any differently. It will simply increase and decrease the speed as needed. See an example of floating control:
The downside to floating control is that there is no proportional control. It will not take a bigger step size when the error is high. To combat this, and especially to aid during startup of equipment, this floating control macro utilizes two different step sizes – one for when error is low, and one for when error is high. By setting the threshold sufficiently high, this will cause more rapid acceleration during startup, and then quickly revert back to normal control during normal operation.
This same code will also work relatively well for any size or nature of supply fan or supply pump. Minor adjustment of the parameters may be needed, but it will give a very decent starting point.
PID
PID control is for control loops of moderate speed. It can be thought of as the "valves and dampers" control method. A chilled water valve modulating to control supply air temperature or a damper modulating to control outside air flow are two examples of when PID control is appropriate.
It is a source of debate whether PID control is appropriate in different situations. Some attest that a PID loop can be tuned to accurately control in any situation, including those where this document recommends either floating or cascade control. While this is certainly true, just because a PID can be used, does not mean that it is always the most appropriate solution, or that it will continue to work even as conditions change.
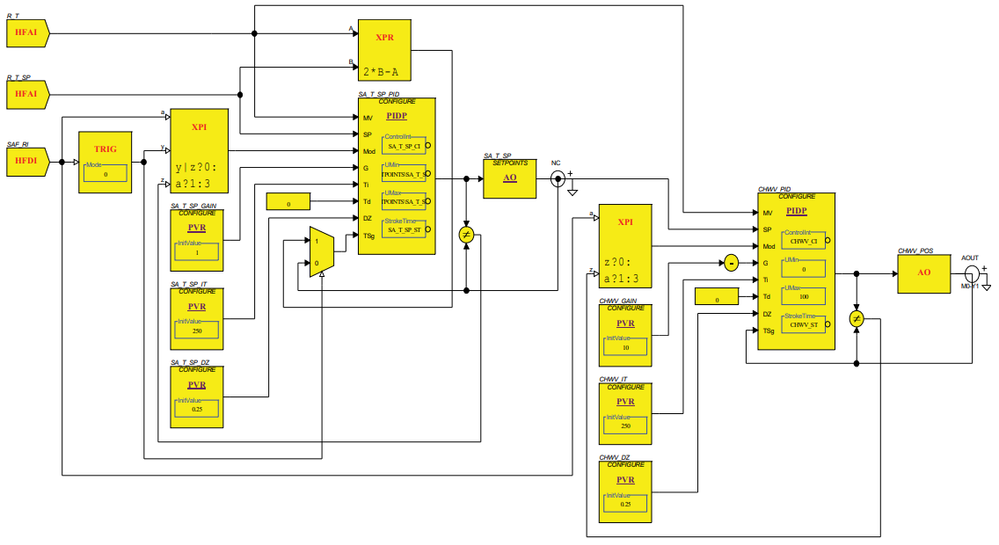
Cascade Control
Cascade control is used in very slow control loops. It is called cascade because two PIDs are used in a cascading arrangement – the output of the first is the setpoint of the second. An example of when to use cascade control is to modulate a chilled water valve to maintain the space temperature in a very large gym or auditorium. A small change in the chilled water valve position could take a very long time to have an effect at the sensor.
If a regular PID is used, it is likely that the PID will wind up all the way to 100% output before the sensor ever experiences the first adjustment's effect. Then it will stay at 100% until it over-cools the space and starts decreasing the call for cooling. The same thing will happen on the reverse side as it modulates all the way to 0% and under-cools the space. And the cycle will continue indefinitely.
In this cascade configuration, the supply air temperature setpoint is modulated based on the room temperature and setpoint. The chilled water valve PID then maintains the supply temperature. This will allow control that is more accurate and prevent the oscillation sometimes seen by inappropriate use of a single PID.
Putting It Into Practice
There are college courses devoted entirely to the subject of PID control. The subjects covered in this document have barely scratched the surface of the topic. The intent is to give the average Menta/Function Block programmer and field technician the information needed to get a system up and running in as little time as possible with the most satisfied customer possible.
Understanding when and why to use PID control will increase accuracy and efficiency of control loops and decrease wasteful overshoot, hunting, and oscillation. Tuning efforts will also be accelerated when the default parameters only require minor tweaking instead of calculation and trial and error.
Using the hints and tips suggested will allow not only for proper programming techniques, but also for creation of macro libraries that can be reused and shared to improve effectiveness across business units.